I've been working in the Data Science / AI space for quite some time now. Longer than I'd like to admit. Given how rapidly the industry has been evolving, I pride myself in being up-to-date on most new techniques. But there are still large parts of the AI landscape I don't get to get my hands dirty.

Reinforcement learning (RL) was one such subdomain I had mostly known at a very high level, and not delved into too deeply. Of course, I knew all about DeepMind and their Alpha Go models that caused a stir when it beat the best human player. More recently, it was also a term making rounds when ChatGPT became a sensation, with a technique called Reinforcement Learning from Human Feedback (RLHF) touted as the reason for its being so good at human-like conversations.

A Challenge awaits

It was around the beginning of last year (2023) that I was asked if I wanted to give a talk/workshop on Reinforcement Learning at a local Smartbot Competition. The competition was a months-long challenge being held by a prominent mobile gaming company in Nepal. Most of the participants were university students, and they were tasked with creating a game bot to play a card game against each other.

Now, I'd normally not give talks on topics I had so little experience with. But this time I said yes. The main reasons being – (1) I wanted to learn how AI game bots were created, and (2) I could finally spend some time learning about Reinforcement learning in some detail, hence increasing my own understanding of how AI models are built today.

In this blog, I'll talk about my presentation and what I learned in the process of creating it.

Thinking in First Principles

When I first started thinking about the topics I would present, it seemed like a choice between picking an algorithm like Q-learning, SARSA, PPO or any of the shiny Deep Learning based ones. But I quickly realized talking for a couple of hours about algorithms that the participants may or may not use in the competition is not what I wanted to do. After all, there are many talks on these topics from people who actually know this stuff.

So, I thought of giving the talk with an approach inspired by the Feynmann technique. I'd implement a game bot myself from scratch, and distil what I learned, the mistakes I'd made. The idea was to teach the students how to think about the problems of creating AI game bots, and enable them to find solutions for their own project.

Because of competition rules and time constraints, I couldn't develop the card game bot itself. So, I choose to implement a bot that could play generalized variations of the board game tic-tac-toe. Not only is tic-tac-toe one of the simplest board game, there are increasingly more complex variations of it, from connect four to gomoku (a much simpler version of go). Thus, allowing me to progressively build more complex bots using ever more sophisticated algorithms.

I titled the talk "Developing AI Game bot from Scratch".

Coincidently, the talk was rescheduled at my alma mater - IOE, Pulchowk Campus. Which made it that bit more special. The rest of the article summarizes what I said that day.

Setting the Stage

First, we need to how to develop the mental model for encoding a computer game as a RL problem.

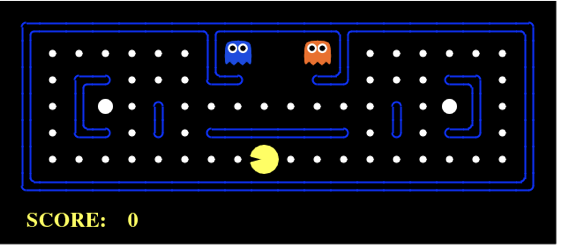
Pac-Man is a game we're all familiar with. Its game states can be used to understand how a game play agent can be framed in a typical RL model.

An agent takes actions in an environment, which is interpreted into a reward and an observation (representation of the state), which are fed back into the agent.

So, in the above scenario, the yellow Pac-Man represents the agent. It can take actions by moving in four directions (up, down, right and left). The actions it can take are defined by the policies of the environment, which is the whole Pac-Man game board itself. In the simplest single player mode, the blue and orange "ghosts" are also part of the environment. The objective of the game is to finish it without getting killed by any of these two adversaries.

Each action taken, is then interpreted by the game environment with rewards. These rewards are either positive or negative. Examples of the positive reward is an increase in score each time it moves through the white dots, power up when it moves past the bigger white dots. A negative reward is it coming in contact with any of the two adversaries. So, the agent is either in an alive or dead state at any given time.

The challenge lies in the fact that the two adversaries can move independently and in a random through the board. Thus, the need for an optimal strategy for each move it makes.

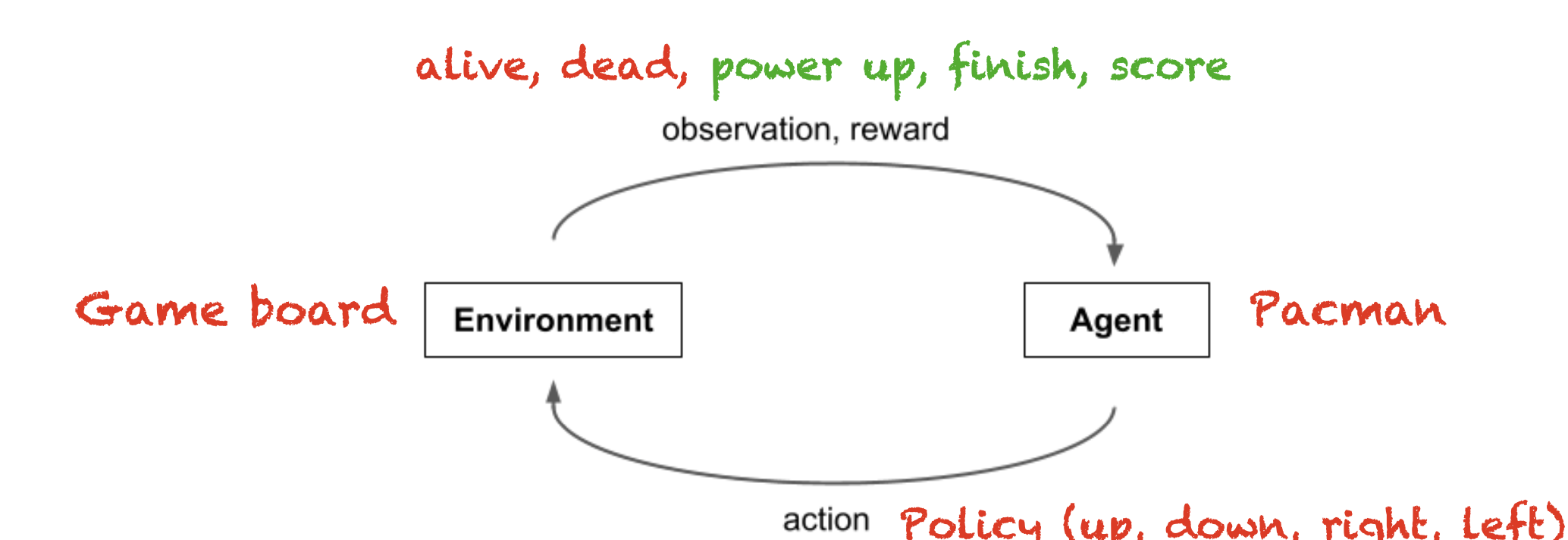
Supervised Machine Learning Analogy

So, the problem of designing optimal game-play bots can be thought of as developing a RL model.

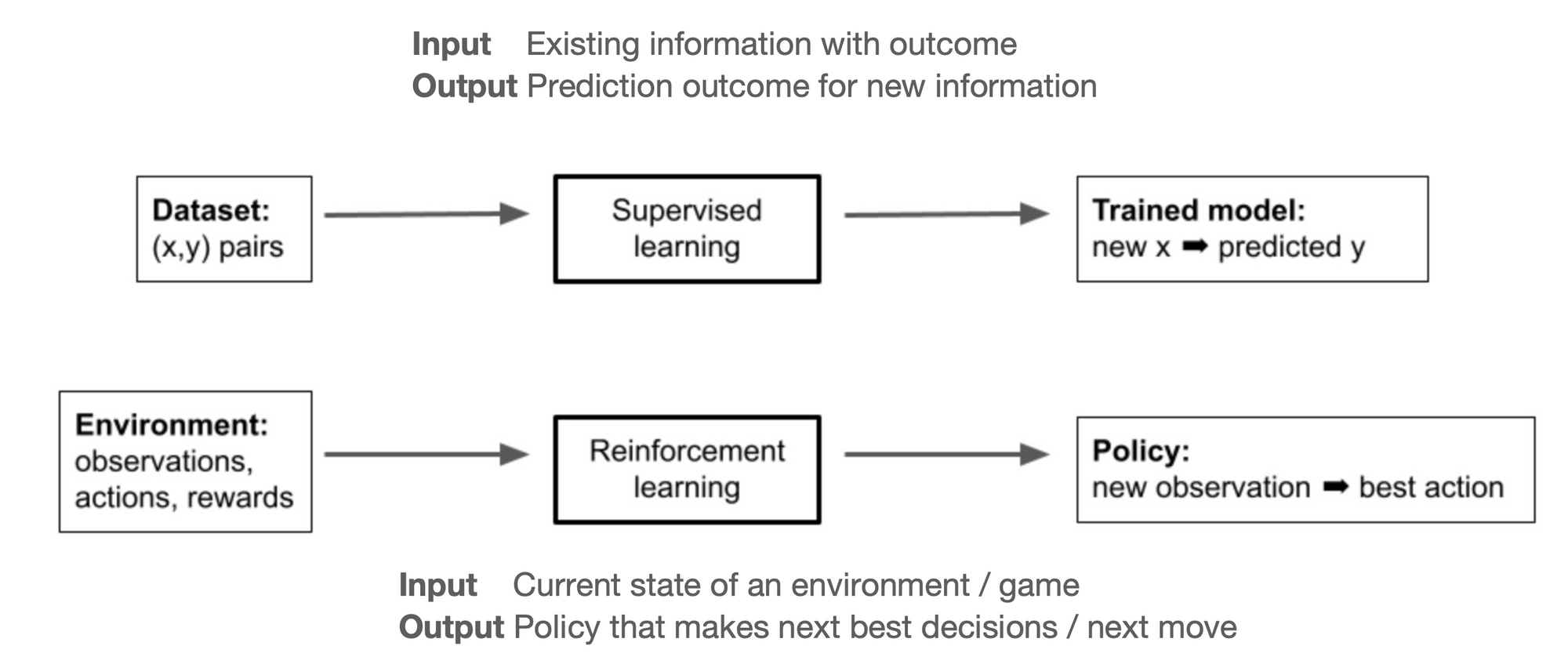
Similar, to how we think of the supervised ML problem as taking existing data whose label is already known, to learn a model that an only take the input features to predict an unknown desired outcome. The RL model can be thought of as the process of learning a policy that can take the existing state of the environment and past actions and rewards of an agent and to output optimal next best action for the agent.

Multi-Agent Games

The next step from a single-agent game, like Pac-Man, are games where more than one player compete against each other for a win. So, these can also said to be zero-sum games, where there's always one winner.

We can see a few examples in the image above. The simplest for of these board games like chess, tic-tac-toe, go, or even some turn-based strategy games. These are called perfect information games, as the complete state of the game is known to all the agents at all time.

In contrast to these games, in most card games (poker) and first-person shooter games (DOTA), each player hides some information from their opponents. These are called imperfect information games.

There are also games that have an element of luck involved, like dice games (ludo), or most casino-style games (roulette).

Developing AI game agents to play against, get progressively more complex for these different types of games. Starting out with multi-agent perfect information games are the next step, and the other methods build on these.

Solving Perfect Games

Before going into writing algorithms, the best way to start any model building is to see the feasibility of writing basic logical rules to solve any problem. Not only are they simpler, computer are really fast at processing rules as compared to deploying ML models.

This is remarkably effective for simple games like tic-tac-toe. I managed to create a fairly competitive tic-tac-toe agent with a strategy to follow two simple rules:

1. start at the center cell if available
2. block the next cell if the opponent has two cells in a row in any orientation.

But, coding hand rules would simply not be feasible for more complex games, and we have to try and go into game solving by computation.

Growing Trees

Most algorithms for game play are based on solving Game Trees. The idea is to iteratively build out / simulate future possible states of a game from the current state, and find the next move (aka tree branch) that results in a win or largest future reward.

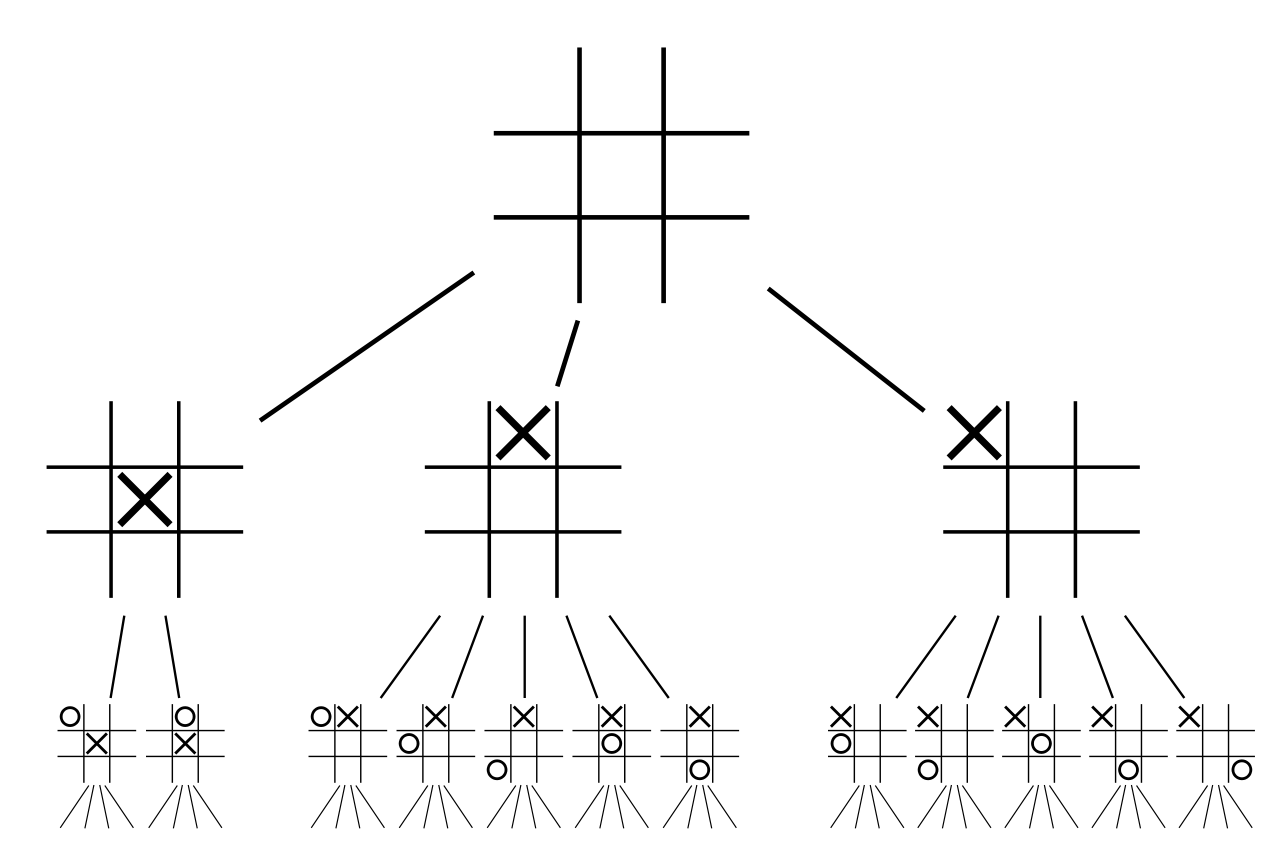
The most popular of these methods is the Minimax algorithm. Here, each player makes a move that maximizes its own reward and/or also minimizes that of the opponent. In my case, this algorithm worked for 3x3 tic-tac-toe, but could not solve a 6x6 variation (connect 4) even after running it for a few hours.

An optimized variation of this algorithm called Alpha-Beta pruning however should work. It was used by the famous IBM Deep Blue to beat Garry Kasparov at chess.

Taking a gamble in Monte Carlo

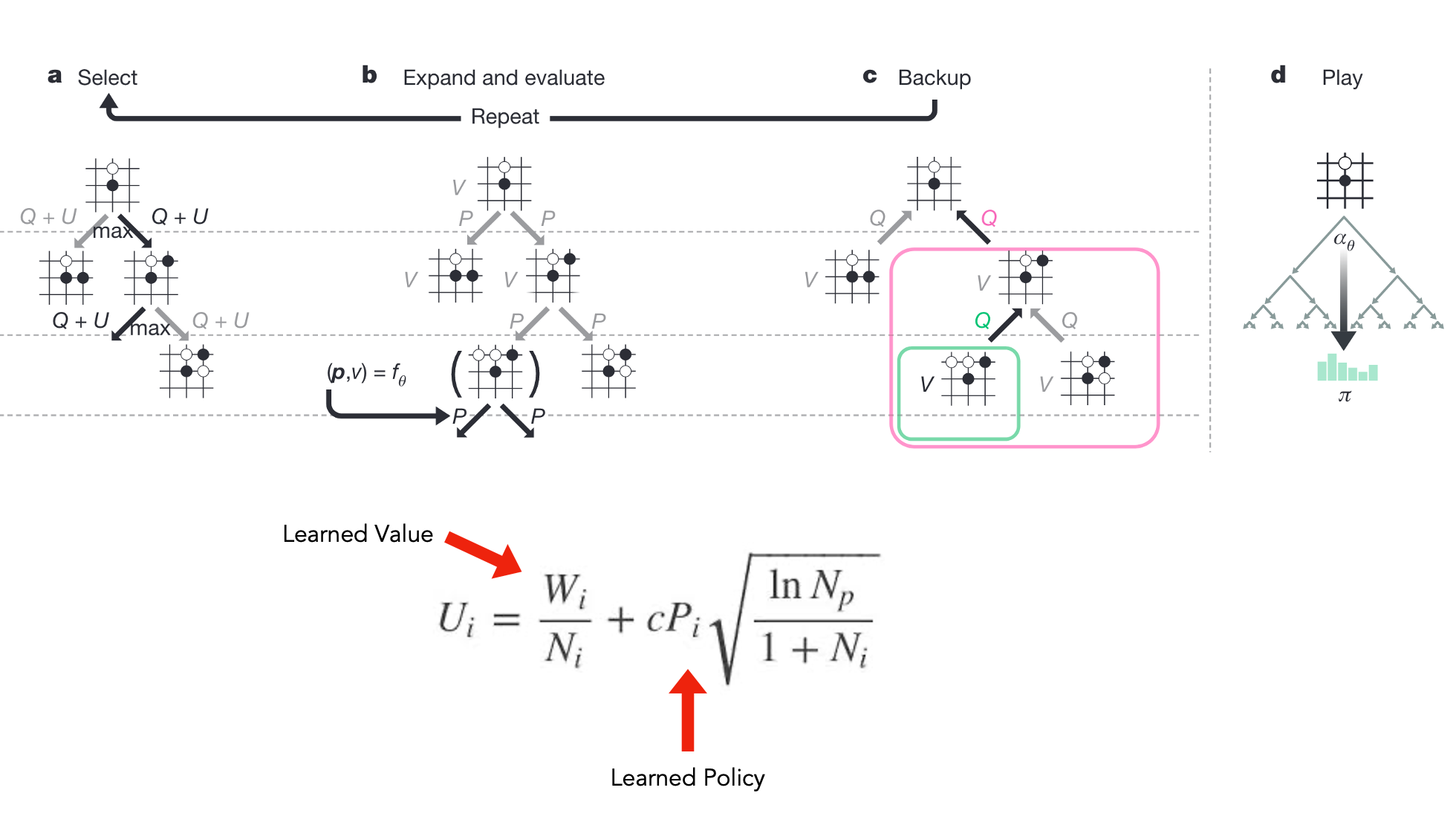
After looking around for more optimal algorithms, I found one called the Monte Carlo Tree Search (MCTS) algorithm. As with anything that has Monte Carlo (a famous casino) in the name, the algorithm uses probability to find the most optimal solution. Even the famous AlphaGo used it in combination with Deep Learning to beat Lee Sedol. So this is definitely worth trying out.

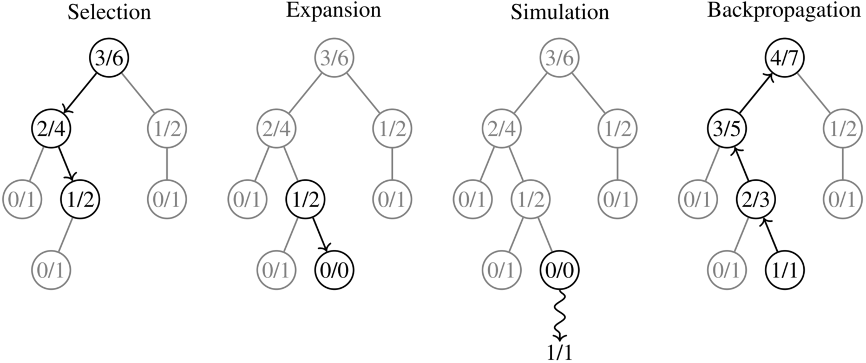
The main difference of the MCTS algorithm is that it does not exhaustively search the game tree. Instead, it is based on the principles of exploration and exploitation.

What this means is that at each given state, it randomly samples different paths and expands the search tree on that path. It then performs simulated moves (called rollouts) to build up statistics up to a certain time or number of child paths. It then exploits moves that are known to work well in order to probe them further. Additionally, it also explores new paths so that it doesn’t get stuck down paths that are yielding good results locally, but missing out on more optimal paths globally.

I build a version of the earlier game-play agent with MCTS and was able to get it to play the 6x6 Connect Four version of it, which the earlier algorithms struggled with.

For my experience, MCTS is a good starting point for anyone building game bots for board games.

How AlphaGo Goes?

After successfully implementing a game bot to play more complex variations of tic-tac-toe, I wanted to understand how AlphaGo does it. One really intriguing part of its algorithm is it enhances the vanilla MCTS algorithm with policies learned from a Deep Learning (neural network) model. This algorithm is called self-play reinforcement learning. It is, dare I say – rather neat.

Earlier versions of AlphaGo used historical records of games played by humans against each other for this. Later on, they used games of AI vs AI instead. So, the first step they took was to take a current (less advanced) version of itself, play many games. Learn more optimal parameters and then repeat this process to have increasingly more sophisticated versions of itself. This phase is called self-play.

The main purpose of this phase is to collect data on previous games to learn how the rules work. Generally, there are two neural networks that are learned by the AlphaGo model: a policy network and value network.

The idea is to use them to guide the search phase of the MCTS algorithm during actual game-play, using the knowledge learned from the historic/self-play games.

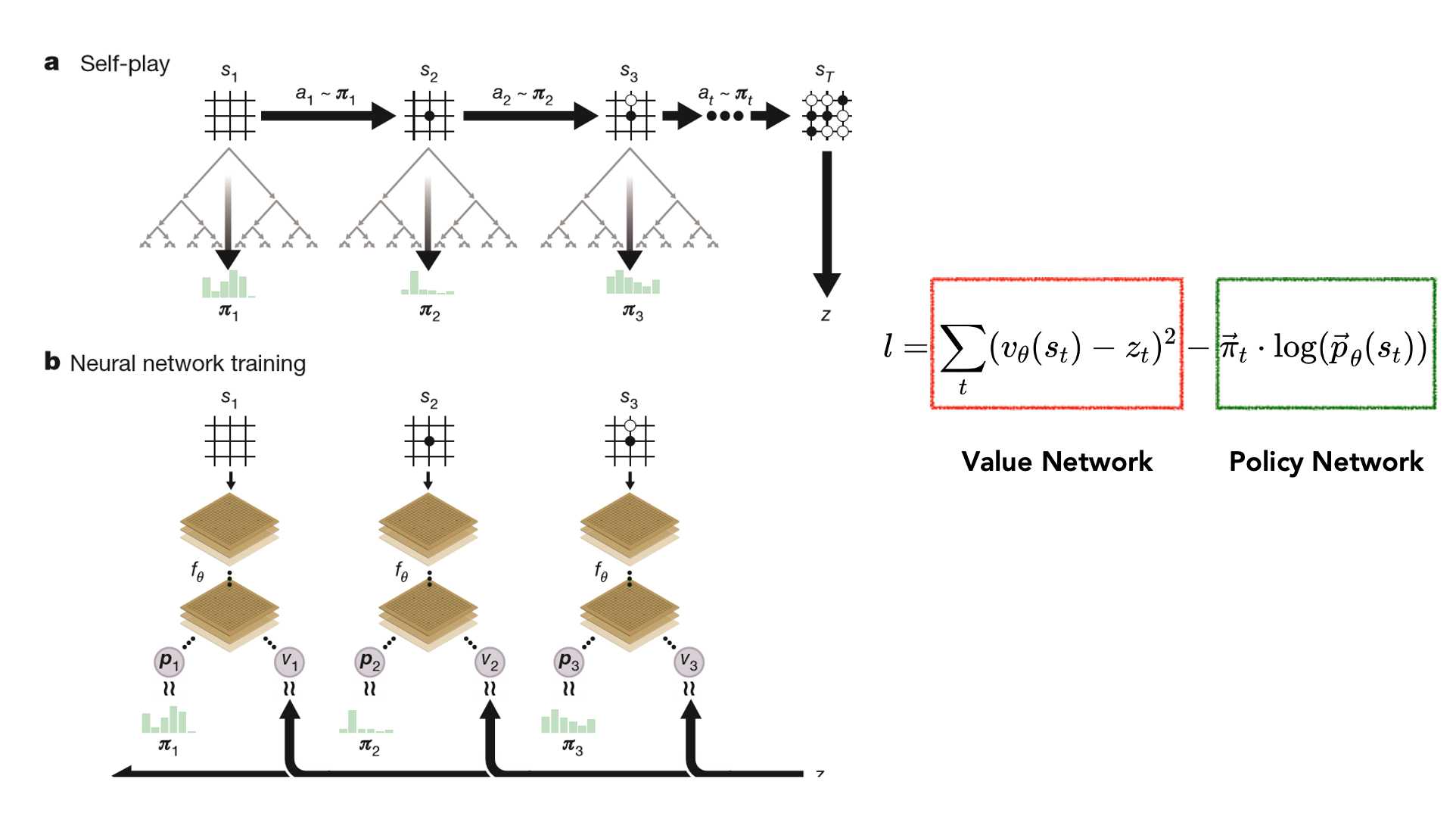
The policy network gives the probability of winning for each subsequent move given a current state, hence minimizing the need to explore many different paths by deciding the next step. The value network provides the actual reward probability for each complete move, hence minimizing the number of paths the algorithm needs to search.

The Omega to your Alpha

Outside to learning how the AlphaGo algorithm works, I also implemented a simpler version myself, called OmegaZero (Oz).

The Oz agent was trained on 1000 self-play games against a randomly initialized version of itself, and using the improved version through 10 epidodes to finally come up with the policy and value networks. This took aroud 6 hours in my basic laptop.

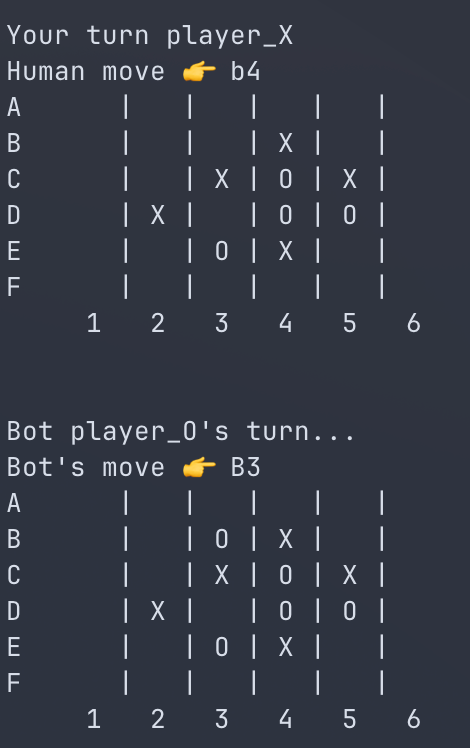
Oz was definitely an improvement over the earlier vanilla MCTS implementation. I also deduced that it was optimizing for winning rather than blocking me from winning the games, and prefers winning diagonally. This can be seen in the move it did above.

I plan to train it further, and see what nuances it learns.

Solving Imperfect Games

After spending almost a week on getting from a simple rule-based tic-tac-toe to OmegaZero, I didn't really get time for actually implementing card game bots. As I stated earlier, given the nature of most of these games these are imperfect information games. Each player knows about the cards in its hand and those that came earlier, but does not really know exactly what the other player's cards are. This is also what real-world is like. For example, when we build economic models.

To go about finding solutions for these type of games, we need to look at the simplest example of an imperfect information game. From what I could find this was rock-paper-scissors.

So, the basic strategy in this game is to – use your knowledge of past games played with the same opponent(s), and look at game theory.

The first method entails fully learning the opponent model and treat it as an single-player game.

The game theoretic approach assumes a game play strategy of Nash Equilibrium. Here each agent learns best response to other players. Essentially, one player’s policy determines another player’s environment, and all players are adapting to each other.

An interesting anecdot was learning that for the Rock-Paper-Scissor game, research has found an approach of 40% rock, 40% paper and 20% scissor will win you more games.

Some algorithms to look into

Two popular algorithms that I found being used to create game bots for these type of games are:

1. Information Set MCTS
2. Monte Carlo Couterfactual Regret Minimization (CFR)

Both of these are more advanced variations of our earlier algorithms. I will explore them and write about them here in the future.

This brings me to the end of this journey I went through building AI game bots. It is also a reminder for me to continue exploring the more advanced algorithms, and develop something useful that I can share. Stay tuned.

As a bonus, if you subscribe to the newsletter, you will receive a pdf copy of the slides from the talk. Please subscribe to receive that right in your inbox.

Any feedback and comments are most welcome.